英語2列（PA)：ALESS

Shoe soles are mostly made of thermoplastic rubber (TPR) because of its light-weight, durability, flexibility, and slip resistance; however little is known about exactly what shape the shoe sole should take in order to provide the optimal amount of friction between the shoe sole and the ground for maximum comfort. To shed new light on this lacuna in our knowledge, the proposed research will use rubber for repairing shoe soles and measure the amount of force needed to slide rubber soles as well as to completely slide the rubber soles off from a single stair step under three alternative conditions, two of which represent the state of walking and running, respectively. Furthermore, the amount of force needed to slide the rubber soles and to completely slide it off from a single stair step will be measured for various degrees of lubrication between the shoe sole and the stair step; this experiment is intended to simulate a lack of traction due to rain. The results may find application in designing less slippery shoe soles for both sunny and rainy days.

References

Resource Library: Shoe Sole Materials

http://www.large-size-shoes-for-men.com/shoe_soles.html

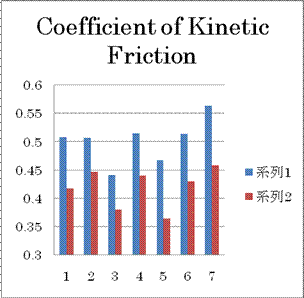
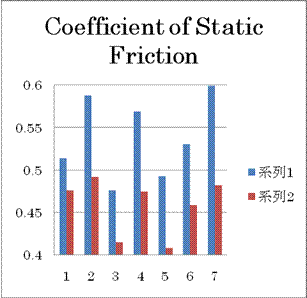
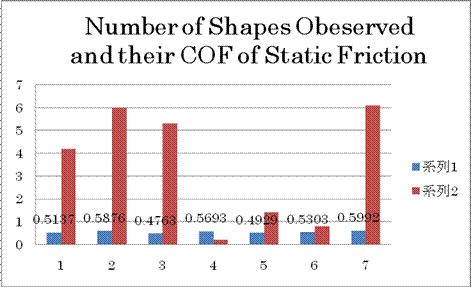
The coefficient of friction (COF) measured in this experiment is defined in Wikipidia (3 December, 2008) as the ratio of the friction to the normal force, the perpendicular force compressing two parallel surfaces together. For the COF of static friction, the maximum friction force applied before the surfaces slide is used. It is used to approximate the value of friction between any two given surfaces; generally the COF of static friction is greater than that of kinetic. The COF varies depending on the temperature and the velocity of sliding on the surface, whereas it is independent of surface area.

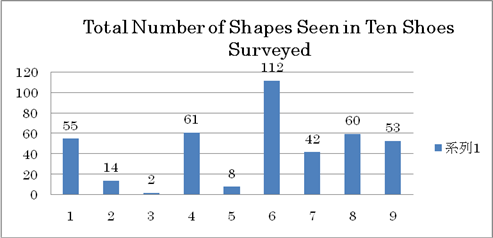
                Out of ten random shoe soles I surveyed[i], lines were the most common pattern found on shoe soles, with an average of 11.2 lines per shoe, followed by trapezoids and circles with 6.1 and 6.0 shapes per shoe, respectively. Rectangles and squares were often seen in clusters with a relatively high average of 5.5 and 5.3 shapes per shoe, respectively. Despite the fact that some sport shoe soles consist only of hexagons, hexagons were least recorded with an average of 0.2 hexagons per shoe. Semicircular shapes, typically used in high heel soles, had a low average of 0.8 semicircular shapes per shoe in the rest, mostly used to fill in empty spaces.

To investigate the correlation between the shape of the surface in contact and the coefficient of friction (COF), I measured the amount of force needed to start rubber soles of various shapes to slide from a stationary state, as well as to keep them sliding, and calculated the COF. Rubber shoe soles were cut into seven distinctive shapes observed in my survey of shapes found in shoe sole patters: triangles, circles, squares, hexagons, crosses, semicircles, and trapezoids. For each experimental replicate, rubber soles were attached to a kitchen scale with string, and pulled horizontally on the ground. Weights were placed on top of each rubber sole to amplify the friction force, which makes the differences more perceptible. Next, I conducted an otherwise identical experiment with the floor wet; this experiment is intended to simulate the lack of traction due to rain. Five trials were performed with all possible combinations of distinctive shapes and wet or dry floor.

              I found that the coefficients of static friction varied more with different shapes, than did the coefficient of kinetic friction. For both COFs, the trapezoid rubber sole exhibited the largest COFs (0.5992 for static friction, 0.5643 for kinetic friction both with a dry surface), followed by the circle and the hexagon. On the other hand, the square rubber sole exhibited the least COFs (0.4763 for static friction, 0.4415 for kinetic friction both with a dry surface), followed by the cross. Compared with the number of shapes observed in shoe sole patters in my survey, the results show that shapes that have greater static friction tend to be used more frequently in shoe sole patterns, though there are exceptions such as the hexagon and the square. Furthermore, there was a 16 percent (0.08) decrease on average in both COFs, when the floor was wet; this confirms the lack of traction between shoe soles and the floor due to rain, as measured by the COFs.

              In the production of shoes, however, the shapes on shoe soles patterns are likely to be determined not only by the size of friction force resulting from particular shapes in contact with the ground, but also by the easiness of spatial orientation of the shape itself. Although circles and hexagons have similar COFs, circles are considerably more common in conventional shoe sole patterns, presumably because of its easiness of spatial orientation. While both circles and hexagons are symmetric and therefore are relatively easy to distribute spatially, circles are more likely to fit easily with other shapes. Squares and rectangles are seen in clusters not only because it increases the total amount of friction force but presumably because it is relatively easier to place rectangular shapes in high density.

These results suggest that regulating the configuration of shapes may open a new door to controlling the friction force between two surfaces, aside from the popular way of modifying the material itself. Frictional force plays an important role in determining and therefore regulating the strength and stability of precision instruments and engines. My results, for example, suggest that trapezoids should be used for curves in order to achieve maximum friction force, whereas semicircular shapes may be the best way to decrease friction force without adding lubrications. Regulation of friction force by arranging shapes in their expedient configuration may have applications in manufacturing more competent precision instruments and engines.

Shoe soles are mostly made of thermoplastic rubber (TPR) because of its light-weight, durability, flexibility, and slip resistance[１]; however little is known about the correlation between the pattern or shape and its friction force. Thus I measured the amount of force needed to start rubber soles of various shapes sliding from a stationary state, as well as to well as that of kinetic friction. Here I will show how the pattern and shape of a surface is closely related to its friction force; the coefficient of static friction varies more by the shape of the surface in contact than the kinetic friction. Conventional shapes in shoe sole patterns are therefore deliberately configured by shapes that are easy to orient in space, and achieve the optimum amount of friction to provide maximum comfort. Regulating friction force by arranging shapes in an expedient configuration may have applications in manufacturing more effective precision instruments and engines.